Misurare le grandezze

http://www.ufottoleprotto.com/fisica_5.htm

 - Dalle osservazioni alle grandezze e unità di misura:

L'osservazione è il primo passo fondamentale per l'indagine scientifica. 
Chiamiamo osservazioni scientifiche le informazioni che vengono raccolte in modo sistematico, controllate e messe a confronto tra loro.
Vengono chiamate grandezze le proprietà misurabili dei corpi, cioè quelle che possono essere sottoposte all'operazione di misura, quindi tutte le proprietà misurabili.

L'unità di misura è una quantità della stessa specie di quella presa in esame, il cui valore viene stabilito pari a 1.
L'unità di misura del sistema internazionale ( SI) si dividono in grandezze fondamentali e grandezze derivate.

MISURE DIRETTE E INDIRETTE

• La portata: di uno strumento di misura è uguale al massimo valore della grandezza che si può misurare con quello strumento.
• La sensibilità: di uno strumento di misura è uguale alla minima variazione della della grandezza da misurare, rilevabile dallo strumento.
• Le misure dirette: si ottengono confrontando la grandezza con la sua unità di misura; le misure indirette si ottengono con calcoli matematici.

MISURE DI SUPERFICIE E DI VOLUME

Della grandezza derivano le seguenti grandezze:

1. Superficie
2. Volume
3. Volume dei liquidi

•  Superficie

La misura di una superficie è l'aria.

L'unità di misura principale della superficie è il metro quadrato che viene indicato con la sigla mq oppure con m².

Il metro quadrato corrisponde ad un quadrato il cui lato è lungo 1 metro.

Riportiamo, nella tabella che segue, i MULTIPLI  e i SOTTOMULTIPLI del metro quadrato con le rispettive sigle.

MULTIPLI			UNITA' DI MISURA	SOTTOMULTIPLI
chilometro quadrato	ettometro quadrato	decametro quadrato	metro quadrato	decimetro quadrato	centimetro quadrato	millimetro quadrato
km2	hm2	dam2	m2	dm2	cm2	mm2
1.000.000 m2	10.000 m2	100 m2		0,01 m2	0,0001 m2	0,000001 m2

Come si trasforma una misura di superficie in un'altra? Per farlo dobbiamo tenere presente la tabella che abbiamo appena visto e ricordare che:

• per trasformare una unità di superficie in un'altra di ordine superiore dobbiamo spostare la virgola verso sinistra di tante coppie di cifre quanti sono i posti che intercedono tra le due unità di misura;

Esempio:

513,8 m² = 5,1380 dam²

71831,7 m² = 7,183170 hm²

3218,15 mm² = 32,1815 cm²

• per trasformare una unità di superficie in un'altra di ordine inferiore dobbiamo spostare la virgola verso destra di tante coppie di cifre quanti sono i posti che intercedono tra le due unità di misura.

Esempio:

5,12 m² = 512 dm²

2,726 hm² = 272,60 dam²

435,30 cm² = 43.530 mm².

• Nel caso in cui dovesse essere necessario, si aggiungono degli zeri, se il numero delle cifre non è sufficiente.

       Esempio:

      6 m² = 0,06 dam²

      0,04 dam² = 400 dm².

•    Volume

La misura di un solido prende in nome di volume.

L'unità di misura di volume principale è il metro cubo che viene indicato con la sigla m³.

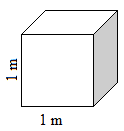
Il metro cubo corrisponde ad un cubo il cui spigolo è lungo 1 metro.

Riportiamo, nella tabella che segue, i MULTIPLI  e i SOTTOMULTIPLI del metro cubo con le rispettive sigle.

MULTIPLI	UNITA' DI MISURA	SOTTOMULTIPLI
decametro cubo	metro cubo	decimetro cubo	centimetro cubo	millimetro cubo
dam3	m3	dm3	cm3	mm3
1.000 m3		0,001 m3	0,000001 m3	0,000000001 m3

I multipli del metro cubo sono poco utilizzati e si è soliti impiegare solamente il decametro cubo.

Come si trasforma una misura di volume in un'altra? Per farlo dobbiamo tenere presente la tabella che abbiamo appena visto e ricordare che:

• per trasformare una unità di volume in un'altra di ordine superiore dobbiamo spostare la virgola verso sinistra di tanti gruppi di tre cifre quanti sono i posti che intercedono tra le due unità di misura;

Esempio:

1.508,8 m³ = 1,5088 dam³

13.850,7 dm³ = 13,8507 m³

3.125.360,7 mm³ = 3,1253607 dm³

• per trasformare una unità di superficie in un'altra di ordine inferiore dobbiamo spostare la virgola verso destra di tanti gruppi di tre quanti sono i posti che intercedono tra le due unità di misura.

Esempio:

512,321 m³ = 512.321 dm³

2,7261 cm³ = 2726,1 mm³

4,353022 m³ = 4353022 cm³.

•         Volume dei liquidi    

 I liquidi non hanno forma propria, ma tendono ad assumere la forma del recipiente nel quale vengono riposti. I liquidi essendo incomprimibili hanno un volume costante, nel caso si trovino in un recipiente isolato ( sennò si avrebbero variazioni di volume a causa dell'evaporazione).
Il volume può variare a seguito di un'innalzamento di temperatura per via del fenomeno della dilatazione termica, ma raggiunta una certa pressione il liquido passerebbe allo stato aeriforme. Il volume di un liquido si misura in litri, simbolo L.
 1L =  dm³

^{Un litro ha multipli e sottomultipli decimali:}   

 

-  l'ettolitro (hl):  1hl  = 100 dm³

-  un millilitro (ml):  1ml  = 1cm³

L'ERRORE É PRESENTE IN OGNI MISURA

 La misurazione di una grandezza fisica comporta sempre un errore,qualunque sia la sensibilità dello strumento utilizzato o del metodo di misurazione adottato.


 -  Le cause degli errori:

• distrazione intervenuta al momento della misurazione;
• limite dello strumento (scarsa sensibilità o difetto di funzionamento);
•  metodo di misurazione;
• cause difficilmente contrallabili o prevedibili. 

DISTINGUIAMO  DIVERSI TIPI DI ERRORI

• L'errore banale è causato da uno sbaglio causato durante l'operazione di misura.
• L'errore sistematico si ripresenta sempe nello stesso mod, tutte le volte che si segue una misurazione.
• L'errore casuale è dovuto a cause sconosciute oppure è provocato da fenomeni di cui è impossibile prevedere gli effetti.

VALUTARE L'INCERTEZZA DI UNA SERIE DI MISURE

• La media aritmetica si calcola sommando tra loro i valori delle misure e dividendo il risultato per il numero n delle misure.

          

• La dispersione d dei valori  misurati di una grandezza è la differenza tra il valore massimo e il valore minimo di una sequenza di misurazioni. 

         - dispersione:  d =  Xmax -  Xmin    

•  L'errore assoluto errass del valore medio è uguale alla dispersione delle misure effettuate divisa per due.

        -  errore assoluto:  errass =  d/2

• L'errore relativo errrel di una misura è uguale all'errore assoluto diviso per il valore medio della grandezza.

        -  errore relativo:  errrel = errass / media (m)

• L'errore percentuale e% di una misura è uguale all'errore relativo moltiplicato per 100.

       -  errore percentuale:  e% = errrel x 100

• L'errore assoluto di una singola misura è uguale alla sensibilità dello strumento utilizzato per eseguire la misurazione. 

L'ERRORE SU MISURE ATTESE E SU MISURE DIRETTE

•  L'errore  assoluto su una misura attesa è la differenza tra il valore misurato della grandezza e quello "atteso".
• L'errore relativo su una misura attesa è il rapporto tra il valore assoluto e il valore atteso.
• se due grandezze vengono sommate o sottratte tra di esse, assoluto del risultato è uguale alla somma degli errori assoluti delle singole misure.
• Se due grandezze vengono moltiplicate o divise tra di esse, l'errore relativo del risultato è uguale alla somma degli errori relativi delle singole misure.